ここに円弧と線分で囲まれた図形があります
簡単に言うと、平たい「かまぼこ形」ですね
高さは底辺の20分の1です

たとえば、底辺が20cmだとすると高さは1cmになるわけですが
このときの円弧は、直径が何cmの円の一部でしょうか？

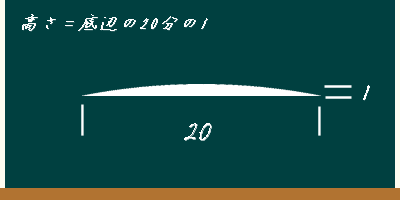
ええっと、実は、かなり前から悩んでいるのですよ

というのも、この形を縮小拡大して使う用事がたまにあるのですが
いつもデザイナーが描いた元の絵から電卓で縮拡率を計算して
コピー機で使いたい大きさにするのですが
大きな白い紙の上で切り貼りするならそれでもいいのです
いや、コピーのかすれや歪みが出てあんまりよくないし
PCの画面でレイアウトするときは
変に縮小拡大するとギザギザが目立ってうまくないんですよ

で、「底辺を○cm(ピクセル)にしたいなら円の直径は○cm(ピクセル)だ」と
即座に判る公式はないものでしょうかねぇ？

---

しばらく、ブログのトップに掲示しておきますので
どなたかお判りの人がいらっしゃったらお教えください

…もし、「こんなの中学生レベルの問題」でしたら
　恥ずかしいので、鍵コメで書き込んでくださいね (^^ゞ